| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- BNK저축은행
- 데이터분석
- 통계독학
- 우리금융캐피탈
- 컨버티드
- 우리금융캐피탈면접
- 빅분기 실기
- 실기1유형
- sql
- 데이터분석마인드셋
- 빅분기1유형
- 빅데이터분석기사
- 빅분기
- 빅데이터분석기사 실기
- 빅분기실기
- 데이터리안
- 우금캐
- 데이터분석전문가
- 투자도서
- boostcourse
- MySQL
- 정처기
- 투자마인드
- 우금캐면접
- 메타코드m
- 데이터분석가
- 빅데이터분석기사실기
- 데이터넥스트레벨챌린지
- 메타코드
- 데이터자격증
- Today
- Total
하파와 데이터
[Day2] Chapter1. EDA(p.32~47) 본문
두번째 글을 올린다. 첫날 공부했던 양인데, 나눠서 올린다.
공부를 해두었고, 글을 올리는것만 하는 것인데도 참 번거로움이 느껴진다.
그러나, 하기로 했으니 우선 계속 해보는게 어떨까라는 마음으로 다시
그러나 사실 지금 30일째도, 50일째도 아닌 2일차라는게 놀랍다..
Chatper1.
1.1 정형화된 데이터의 요소
1.2 테이블 데이터
1.3 위치 추정
1.4 변이 추정
1.5 데이터 분포 탐색하기
1.6 이진 데이터와 범주 데이터 탐색하기
1.7 상관관계
1.8 두 개 이상의 변수 탐색하기
1.9 마치며
1.4 변이추정(Variability)_데이터의 산포(변이)를 추정
학문을 습득하고, 배움을 익히는데 어려운 가장 큰 장애물 중 하나는 그들만의 체계/언어이다.
한국어를 모국어로 사용하지만, 부끄럽게도 우리나라의 9품사에 대해 명확히 모를때가 많다.
더불어 영어를 학습하면서도 분사, 타동사라든지 문법적 용어를 명확하게 모르는 경우가 많다.
그럼에도 영어 문장을 이해하는데 큰 어려움이 없고, 우리나라말을 사용하는데 부족함이 별로 없다.
학문적 체계를 구축하고, 새로운 사람에게 용어로 알려주기위해서 필요할수는 있으나, 이런 용어가 학습을 오히려 더 어렵게 한다는 생각이 든다.
그 일례로, 변이추정이라는 말이 그러하다. 도대체 무슨 말인가.
오히려 영문이 더 이해가 잘 될 때가 있다.
변화가 되는 가능성 정도로 이해하면 되며, Variability를 사전에 검색하면
산포도가 나온다. 즉, 데이터의 값이 얼마나 분포되어있는지를 나타내는 것이다.
여기는 통계의 기본적인 용어에 대한 이해가 필요하다. 우리가 변이(variability)를 받아들인 것처럼
아래의 용어도, 도대체 무슨뜻이야! 라고 묻기보다는 '아 이렇게 부르기로 약속했구나'정도로 받아들이는게 우선일 것 같다.
Deviation(편차): 관측값과 위치 추정값 사이의 차이(추정값과 얼마나 떨어져 있나요?)
Variance(분산): 평균과 편차를 제곱한 값들의 합을 n-1로 나눈 값(내 데이터는 평균으로부터 얼마나 떨어졌나요?)
Standard Deviation(표준편차): 분산의 제곱근
간단히 예시를 통해 알아보기 위해 데이터를 하나 상정해보자.
dt = {1, 4, 4}
평균dt = (1+4+4)/3 = 3
중앙값dt = 4 = 정렬 후 가운데 값
편차dt = {-2(1-3), 1(4-3), 1(4-3)}(각 데이터 - 평균dt)
우리는 각각의 데이터의 편차도 중요하지만, 전체적으로 나의 데이터가 얼마 정도의 편차를 가지고 있는 편이지?를 알고 싶다. 그래야 내 데이터의 전체적 편향성 등을 알 수 있기 때문이다. 하지만 그렇다고 편차를 모두 더하게 된다면?
중학생때 배웠고, 방금 위의 예시를 보면 알겠지만, 편차의 합은 항상 0이 된다.
평균은 모든 데이터를 고려했을때 정확히 가운데에 위치하기 때문에, 각 데이터와 평균과의 거리차이를 듯하는 편차의 합은 항상 0이 되는 것이다.
그렇다면 우리는 무엇으로 데이터를 파악할 수 있을까? 크게 2가지 방법이 있다.


우선 편차에 절대값을 이용하여 평균을 구하게 되면, 음수값이 없어지기 때문에, 편차의 합이 0이 되지 않기 때문에 값을 구할 수 있다.
두번째 방법은 익히 알고 있는, 얼마나 퍼져있는지 확인하는 분산, 분산의 제곱근인 표준편차를 이용하여 확인하는 것이다.
다만, 우리가 바로 전 글에서 확인했던 것처럼 Roburst라는 개념이 있다. 즉, 데이터의 극단값, 이상값에 얼마나 민감한가.
로버스트한 경우를 민감하지 않다. 민감한 경우를 로버스트 하지 않다고 표현한다.
예를들면 평균은 로버스트 하지 않고, 중앙값은 로버스트하다. 아래 글을 참고하면 내용을 조금 확인할 수 있다.
2024.09.10 - [스터디/[독학]데이터분석을 위한 통계] - [Day1] Chapter1. EDA(p.20~32)
[Day1] Chapter1. EDA(p.20~32)
Chatper1.1.1 정형화된 데이터의 요소1.2 테이블 데이터 1.3 위치 추정1.4 변이 추정1.5 데이터 분포 탐색하기1.6 이진 데이터와 범주 데이터 탐색하기1.7 상관관계1.8 두 개 이상의 변수 탐색하기1.9 마
hhpp.tistory.com
아쉽게도, 분산, 표준편차, 평균절대편차는 로버스트 하지 않다. 즉, 특이값에 민감하다. 이럴수 밖에 없는 이유는 바로 저 모든 계산에서 활용되는 근간이 로버스트 하지 않은 평균이기 때문이다. 가장 기초가 되는 값이 로버스트 하지 않은데, 그 값을 활용한 다른 값이 로버스트 하다는 것은 성립하지 않는다.
그럼에도 분산과 표준편차를 많이 활용한다. 쉽고 편리하기 때문이다. 그렇다면 로버스트한 변이 추정방법은 무엇이 있을까? 바로 MAD(Median Absolute Deviation)이다.
MAD는 중앙값을 기준으로 편차를 구하고, 그 편차와 각 데이터의 값을 더한 뒤 데이터의 수만큼으로 나눠주는 것이다.
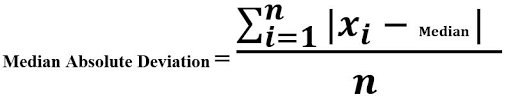
그러면 각 변이추정 값들의 로버스트함(민감도)을 보면 어떨까?

표준편차가 가장 큰 민감도를 보여주고, 중위 절대편차(MAD)가 가장 낮은 민감도를 보여준다.
1.4_2 백분위수에 기초한 추정
추정된 위치로부터 전체 데이터를 보는 방금의 방법만이 유일한 방법일까?
그렇지 않다! 데이터 전체를 정렬해둔 뒤, 비율로 얼마나 퍼져있는지를 확인하는 방법도 존재한다. 그것이 바로 지금부터 알아볼 백분위수에 기초한 추정이며, 이를 순서통계량이라고도 한다.
단, 순서통계량은 평균을 구할때, 절사평균을 구했던 것처럼 극단값으로부터의 영향성을 제거하기 위해 일정비율(P%)를 제거한 뒤 사용하는 것도 가능하다.
이러한 순서통계량에서 가장 대표적인 방법이 상자도표, IQR이다.
이번에도 데이터를 상정해서 이를 확인해보자

D라는 배열이 있다면, 우선 정렬하는 것이 첫번째.
정렬이 끝나면, 1사분위, 2사분위, 3사분위를 각각 나누어 데이터를 확인하는 것이다.
이를 활용하는 방법은 아래 데이터 분포 탐색하기에서 더 확인해본다.
1.5 데이터 분포 탐색하기

여기서 주의할 점은,
1. 상자그림
- 상자의 아랫부분은 1사분위(25%)를, 상자 가운데 선은 2사분위(50%)를, 상자의 윗선은 3사분위(75%)를 뜻한다는 점.
- 상자를 기준으로 위 아래의 선은, IQR(3사분위 - 1사분위 *1.5)만큼의 거리를 나타냄
- IQR을 초과하는 데이터들은 점으로 표현되며, 해당 데이터들은 일반적으로 특이값(Outlier)라고 본다.
2. 히스토그램
- 히스토그램의 막대 사이에는 간격이 존재하지 않는다. 이는 막대그래프(boxplot)과의 기본적인 차이이다.
- x축은 변수 범위를 동일한 크기로 나눈 구간으로, x축은 하나의 변수만을 표현한다. cf) 막대그래프는 다양한 변수 값을 표현할 수 있다.
- y축은 x축에 해당하는 개수가 몇개인지를 보여준다.
3. 밀도그램
- 히스토그램과 동시에 표현할 수 있으며, 연속된 선으로 표현한다.
- 단 차이점은 y값이 다르다는 점. 히스토그램은 개수를 표현하는 반면, 밀도상자의 y는 비율을 표현한다.
1.6 이진 데이터와 번주 데이터
여기에도 기본적인 용어가 나온다.
Moda(최빈값): 데이터에서 가장 많이 등장하는 값
Expected Value(기댓값): 범주에서 해당하는 어떤 수치가 있을때, 범주의 출현확률에 따른 평균
Bar Chart(막대그래프): 각 범주의 빈도수 혹은 비율을 막대로 나타낸 그림
Pie Chart(파이차트): 각 범주의 빈도수 혹은 비율을 원의 부채꼴 모양으로 나타낸 그림

'스터디 > [독학]데이터분석을 위한 통계' 카테고리의 다른 글
| [Day1] Chapter1. EDA(p.20~32) (1) | 2024.09.10 |
|---|---|
| [Day0] 데이터 과학을 위한 통계, 책을 꺼내들어보자 (0) | 2024.09.10 |


