| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 실기1유형
- 우금캐
- 데이터리안
- 데이터넥스트레벨챌린지
- 컨버티드
- 통계독학
- 데이터분석마인드셋
- 빅데이터분석기사실기
- 데이터분석가
- 데이터분석
- sql
- 메타코드m
- 빅데이터분석기사
- MySQL
- 우리금융캐피탈
- 빅데이터분석기사 실기
- 우금캐면접
- 투자도서
- boostcourse
- 빅분기실기
- 빅분기1유형
- BNK저축은행
- 우리금융캐피탈면접
- 데이터분석전문가
- 정처기
- 메타코드
- 빅분기 실기
- 투자마인드
- 데이터자격증
- 빅분기
- Today
- Total
하파와 데이터
[빅분기] 실기 1유형- 수치형 데이터 분석(개수, 최소, 최대, 평균, 합계, 중앙값, 4분위, 분산, 표준편차,왜도, 첨도) 본문
[빅분기] 실기 1유형- 수치형 데이터 분석(개수, 최소, 최대, 평균, 합계, 중앙값, 4분위, 분산, 표준편차,왜도, 첨도)
hhpp 2024. 11. 27. 00:54오늘은 수치형 데이터의 기본을 분석하는 여러가지를 한번에 때려배워보자
역시나 엄청난 판다스에 의해서, 모든 것들은 한줄에 끝난다.
나머지는 이미 영어로 단어를 다들 잘 알고 있을테니, 왜도와 첨도의 스펠링만 주의깊게 외우면
모든 것은 일사천리로 끝나버린다!!
빅분기 부셔버리자!!!
0. 전제
현재 Jupyter notebook을 켠 폴더 내 data라는 폴더가 있고, 그 안에 iris.csv라는 파일이 있다.
1. 수치형 데이터 분석(개수~첨도)
import panda as pd
# 데이터 불러오기
df = pd.read_csv('data/iris.csv')
# 개수
df.count() # 각 컬럼별 NaN을 제외한 데이터 수
# 최소값
df.min(numeric_only = True)
# 최대값
df.max(numeric_only = True)
# 평균
df.mean(numeric_only = True)
# 합계
df.sum(numeric_only = True)
# 중앙값
df.median(numeric_only = True)
# 4분위 중 2분위(중앙값) 출력
df.quantile(numeric_only=True) # 모든 컬럼의 중위값이 출력
# 4분위 중 1분위수
df.quantile(0.25) # 괄호 내 0~1 사이에서 원하는 값을넣으면 그 위치의 값이 출력
# 분산
df.var(numeric_only=True)
# 표준편차
df.std(numeric_only=True)
# 왜도
df.skew(numeric_only=True)
# 첨도
df.kurtosis(numeric_only=True)
2. 왜도(skewness) 설명
왜도는 데이터의 대칭성을 나태난다.
즉, df.skew()의 값에 따라 데이터가 대칭인지, 왼쪽 또는 오른쪽으로 긴 꼬리를 가지고 있는지 알 수 있다.
- df.skew() = 0; 정규분포와 같이 대칭적 분포
- df.skew() > 0 (양수); 오른쪽으로 긴 꼬리(오른쪽으로 치우침)
- df.skew() <0 (음수); 왼쪽으로 긴 꼬리(왼쪽으로 치우침)
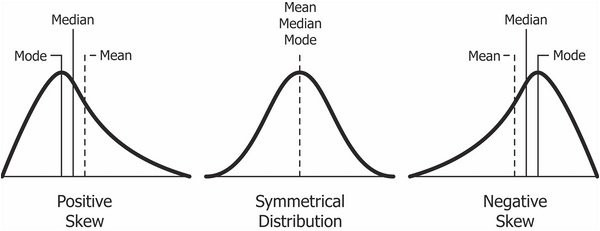
위 사진에서 보는 것처럼, 왜도에 따라서 평균과 중앙값, 최빈값의 위치가 차이를 보이는 특징도 있고, 여러가지가 다 있다. 참고참고!!
데이터 분석을 할때 알아야할 건,
0.5 <= |왜도| <= 1
이렇게 나오는게 괜찮다는 것.
절대값이 1을 넘어간다면, 강하게 치우친 분포를 보이기 때문에 data scaling 등이 필요하다.
3. 첨도(kurtosis) 설명
첨도는 분포의 꼬리 두께를 나타낸다.
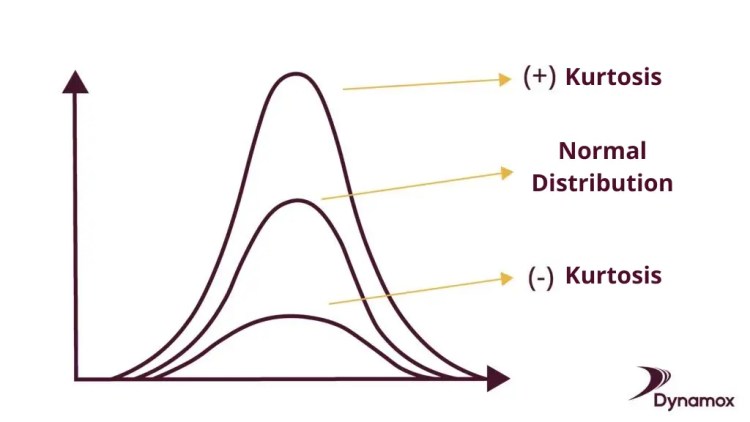
첨도는 왜도와 다르게 3을 기준으로 확인하면 된다.
- 첨도 = 3; 정규분포와 동일한 높이의 그래프
- 첨도 > 3; 그래프의 높이가 낮고, 양 극단값(outlier)이 많이 분포
- 첨도 < 3; 그래프의 높이가 높고, 양 극단값(outlier)가 적게 분포
일반적인 통계에서 첨도는 3을 기준으로 하지만,
pandas에서 kurtosis()는 '초과첨도(Excess Kurtosis)'를 반환한다.
정규분포에서 초과첨도는 = 0이므로
위의 그림과 같이 첨도가 양수면, 높게 솟은 그래프
첨도가 음수면, 낮고 넓게 퍼진 그래프가 된다.
첨도 역시 기준이 있다.
초과첨도를 기준으로 -1<= 초과첨도 <= 1 이 되어야 한다.
4. 왜도와 첨도
하지만, 실제 데이터를 보다보면, 첨도와 왜도의 기준에 부합하지 않을때도 있다.
그래서 여러 실제 데이터 분석 등에서는 조금더 기준을 완화하여
-1 < 왜도 <1
-2 < 초과첨도 <2
이러한 기준을 통과하면 그냥 사용하기도 한단다.
'자격증 > DATA' 카테고리의 다른 글
| [빅분기] 실기 1유형- 데이터 선택; 부분집합(SUBSET) (0) | 2024.11.27 |
|---|---|
| [빅분기] 실기 1유형- 상관계수 (1) | 2024.11.27 |
| [빅분기] 실기 1유형- 결측치 찾기, 고유값 확인, 값 개수 찾기 (1) | 2024.11.27 |
| [빅분기] 실기 1유형- 읽기, 쓰기, Transpose (2) | 2024.11.26 |
| [정처기] 메타코드 강의를 통한 필기 준비! (0) | 2024.11.22 |




